The State of Gaussian Processes in Julia
Currently, the Gaussian process echosystem in Julia is somewhat fragmented. We have GaussianProcesses.jl, which is a standalone package that does just GPs, AbstractGPs that tries to combine multiple GP related libraries into a standardized API, AugmentedGaussianProcesses.jl that provides some advanced GP algorithms on top of AbstractGPs. Unfortunately, none of these libraries currently work on GPUs. This is way behind the norm of Python where GPyTorch supports GPUs quite well.
Here is a summary of the current trends for implementing GPs in Julia.
- Use KernelFunctions.jl for crafting your covariance kernels and computing the Gram matrix.
- Use PDMats.jl for computing the Cholesky, solving systems, computing quadratics, and etc..
- Use AbstractGPs.jl for abstracting all of the GP manipulations.
Frankly speaking,
KernelFunctions.jlis the key here.
The main issue is that most GP libraries (including KernelFunctions.jl) rely on Distances.jl, which is a package for efficiently computing Gram matrices (or distance matrices).
Although Distances.jl is heavily optimized, it’s optimized too much.
It is very difficult to make it compatible with CUDA.jl (an amazing package that is a very good reason to convert to Julia).
This bottleneck has been the showstopper since everbody is pretty much relying on KernelFunctions.jl.
There is some dicussion to ditch Distances.jl in favor of Tullio.jl, but this also has the following downsides:
- It doesn’t support differentiation for complex multiline expressions. It does only symbolic differentiation.
- It’s not very efficient on GPUs, especially for gradients.
So even if
KernelFunctions.jlmoves on toTullio.jl, there is not much to expect at this point.
To summarize,
- GPU support for Gaussian processes on Julia is non-existent.
- Efficient GPU support is not to be expected in the short term.
A Minimal CUDA-Compatible GP Implementation
Overview
Regardless of the current GPU support, I urgently needed GPs to work on GPUs right now. The things we normally expect from GPU support for GPs are these two things:
- faster Gram matrix computation,
- faster Cholesky decomposition,
- faster backward/forward substitution, and
- support differentiation with respect to the hyperparameters and the latent function values
2 and 3 work (pretty much) out of the box in Julia. 1 and 4 is the tricky part. So, I ended up spending a few days writing a few CUDA kernels using KernelAbstractions.jl.
The implementation can be found here.
It supports the two following covariance kernels:
\(\begin{align}
k\left(\mathbf{x}, \mathbf{y}\right) &= \sigma^2 k_{\text{SE ARD}}\left(\mathbf{x}, \mathbf{y} \right) + \epsilon^2
\newline
k\left(\mathbf{x}, \mathbf{y}\right) &= \sigma^2 k_{\text{Matern 5/2 ARD}}\left(\mathbf{x}, \mathbf{y} \right) + \epsilon^2
\end{align}\)
where SE ARD and Matern 5/2 stand for the squared-exponential and Matern 5/2 kernels with automatic relevance determination (ARD), which are, arguably, the most widely used covariance kernels.
We have \(D + 2\) hyperparameters here: the \(D\) ARD length scales, the noise variance \(\epsilon^2\), and the function variance \(\sigma^2\).
Likelihood
The log likelihood of a Gaussian process prior is \begin{equation} \log p\left(\mathbf{y} \mid \mathbf{X}, \mathbf{\theta} \right) = -\frac{1}{2}\mathbf{y}^{\top} \mathbf{K^{-1}} \mathbf{y} - \frac{1}{2} \log \mathrm{det} \mathbf{K} - \frac{N}{2} \log 2 \pi. \end{equation} This is implemented as
function gp_likelihood(
X_dev::CUDA.CuArray{<:Real,2},
y_dev::CUDA.CuArray{<:Real,1},
σ²::Real,
ϵ²::Real,
ℓ²_dev::CUDA.CuArray{<:Real,1},
)
n_data = size(X_dev, 2)
R = distance_matrix_gpu(X_dev, X_dev, ℓ²_dev)
K = matern52_gpu(R)
K_ϵ = eltype(K)(σ²) * K + eltype(K)(ϵ²) * I
K_chol = cholesky(K_ϵ; check = false)
if issuccess(K_chol)
L⁻¹y = K_chol.L \ y_dev
yᵀΣ⁻¹y = dot(L⁻¹y, L⁻¹y)
logdet = 2 * sum(log.(Array(diag(K_chol.U))))
(yᵀΣ⁻¹y + logdet + n_data * log(2 * π)) / -2
else
-Inf
end
endYou can use the squared exponential kernel by swapping matern52_gpu into se_gpu and gram_matern52_derivative_gpu into gram_se_derivative_gpu.
The other routines are self-contained in gpu_cuda_utils.jl.
Hyperparameter Gradients
For the gradients, the GPML (Rasmussen & Williams, 2006) book shows how to differentiate the log likelihood. For the record, the gradients for the kernel hypeparameters are \(\begin{align} \nabla_{\mathbf{y}} \log p\left(\mathbf{y} \mid \mathbf{X}, \mathbf{\theta} \right) &= \mathbf{K^{-1}} \mathbf{y} \\ \nabla_{\epsilon^2} \log p\left(\mathbf{y} \mid \mathbf{X}, \mathbf{\theta} \right) &= \mathbf{y}^{\top} \, \mathbf{K}^{-1} \mathbf{K}^{-1} \, \mathbf{y} - \mathrm{tr}\left( \mathbf{K}^{-1} \right) \\ \nabla_{\sigma^2} \log p\left(\mathbf{y} \mid \mathbf{X}, \mathbf{\theta} \right) &= \mathbf{y}^{\top} \, \mathbf{K}^{-1} \mathbf{K} \mathbf{K}^{-1} \, \mathbf{y} - \mathrm{tr}\left( \mathbf{K}^{-1} \mathbf{K} \right) \\ \nabla_{\ell^2} \log p\left(\mathbf{y} \mid \mathbf{X}, \mathbf{\theta} \right) &= \mathbf{y}^{\top} \, \mathbf{K}^{-1} \frac{\partial \mathbf{K}}{\partial \ell^2} \mathbf{K}^{-1} \, \mathbf{y} - \mathrm{tr}\left( \mathbf{K}^{-1} \frac{\partial \mathbf{K}}{\partial \ell^2} \right), \end{align}\) where, clearly, there is lots of opportunities for reuse. Therefore, writing our own gradients should be far more efficient for GPs both in terms of time and memory.
You can compute the gradients using Zygote as
likelihood_gpu(X_dev, θ) = begin
N = size(X_dev, 2)
ℓσ = θ[1]
ℓϵ = θ[2]
y = cu(θ[3:2+N])
ℓ² = cu(exp.(θ[3+N:end] * 2))
gp_likelihood(X_dev, y, exp(ℓσ * 2), exp(ℓϵ * 2), ℓ²)
end
Zygote.gradient(θ_ -> likelihood_gpu(X, θ_), θ)[1]Note that the gradients with respect to X_dev are not implemented, but shouldn’t be too hard to do.
Demonstration
I will now compare the GPU implementation against AbtractGPs.
I will use 32-bit floating point numbers since most GPUs perform very poorly with 64-bits.
Since I will use my poor little GTX 1050 GPU, the numbers should be much better on a proper workstation with a beefier GPU.
To get proper performance measurements, I turned off frequency scaling and paused Youtube.
(Imagined how bored I was during the experiments.)
Numerical Accuracy
In terms of numerical accuracy, the GPU version is close to the result of AbstractGPs at 1e-4 tolerance level:
Test.@testset "GPU Gaussian process numerical accuracy test" begin
N = 128
D = 16
X = randn(Float32, D, N)
X_dev = cu(X)
θ = randn(Float32, N + D + 2)
@test likelihood_cpu(X, θ) ≈ likelihood_gpu(X_dev, θ) atol=1e-4
@test norm(gradient_cpu(X, θ) - gradient_gpu(X_dev, θ)) ≈ 0.0 atol=1e-4
endComputational Performance
In terms of performance, here is a execution time comparison:
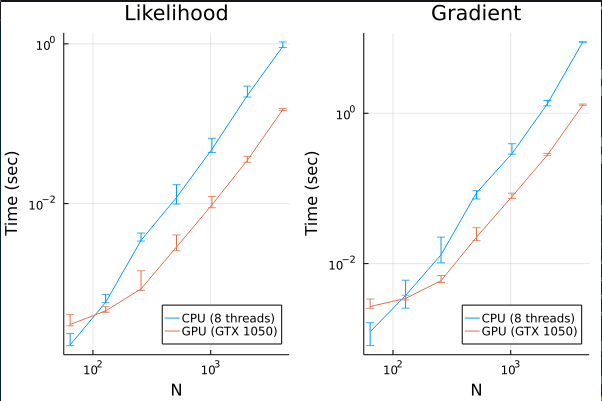
The error bars are the 80% empirical quantiles and \(N\) is the number of datapoints. We can see that GPUs quickly becomes more efficient for \(N>100\). In general, it is about 10 times faster, which is pretty good for a simple implementation without any GPU-specific optimization (not even using shared memory!). Since GTX 1050 is supposed to achieve 1TFLOPS and most modern CPUs achieve around 200GFLOPS, this is close to the most we can get.
Realistic Example
The main.jl file in the repository contains a realistic example with predictions. I performed MAP-II hyperparameter optimization using Optim.jl on the Boston housing dataset. Here are the results:
┌ Info: MAP-II Hyperparameter Optimization Result
│ likelihood_before = -544.3303199616416
│ likelihood_after = -116.86849745187607
│ rmse_before = 0.60338885f0
│ rmse_after = 0.3102568f0
│ lpd_before = -0.8926057396811591
└ lpd_after = -0.16185267732364805
before is the initial hyperparameters used without optimization and after is the result of MAP-II.
We can see that everything is working in order.
Cholesky Fail
When the Cholesky fails, the current implementation does not throw.
Instead, it spits a -Inf for the likelihood and CUDA.zeros arrays for the gradients.
Fixing Zygote for Differentiating Cholesky with CUDA
Update: this has been fixed by sethaxen. See also the issues at ChainRules.jl, Zygote.jl
While doing this, I ran into a bug that prevents Cholesky being differentiated by Zygote, which I reported.
A quick fix is to use the following snippet:
@eval Zygote begin
import CUDA
@adjoint function cholesky(Σ::CUDA.CuArray; check = true)
C = cholesky(Σ, check = check)
C, function (Δ::NamedTuple)
issuccess(C) || throw(PosDefException(C.info))
U, Ū = C.U, Δ.factors
U_tru = triu(U.data)
Ū_tru = triu(Ū.data)
Σ̄ = similar(U.data)
Σ̄ = mul!(Σ̄, Ū_tru, U_tru')
Σ̄ = copytri!(Σ̄, 'U')
Σ̄ = ldiv!(U, Σ̄)
Σ̄ = CUDA.CUBLAS.trsm!('R', 'U', 'T', 'N', one(eltype(Σ)), U.data, Σ̄)
Σ̄[diagind(Σ̄)] ./= 2
return (UpperTriangular(Σ̄),)
end
end
endUpdate: this has been fixed by myself
The weird part of my solution here is the two calls to triu, which create a normal Matrix that is upper triangular, in contrast to the UpperTriangular adaptor.
This is necessary because, currently, multiplying two UpperTriangular matrices on the GPU is extremely slow.
Running the profiler seems to show that there is a weird device memory copy somewhere that takes forever, but I didn’t pursue the matter further.
System Information
julia> versioninfo()
Julia Version 1.7.2
Commit bf53498635 (2022-02-06 15:21 UTC)
Platform Info:
OS: Linux (x86_64-pc-linux-gnu)
CPU: Intel(R) Core(TM) i7-7700HQ CPU @ 2.80GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-12.0.1 (ORCJIT, skylake)
Environment:
JULIA_NUM_THREADS = 8julia> CUDA.versioninfo()
CUDA toolkit 11.6, artifact installation
NVIDIA driver 510.60.2, for CUDA 11.6
CUDA driver 11.6
Libraries:
- CUBLAS: 11.8.1
- CURAND: 10.2.9
- CUFFT: 10.7.0
- CUSOLVER: 11.3.2
- CUSPARSE: 11.7.1
- CUPTI: 16.0.0
- NVML: 11.0.0+510.60.2References
-
Gaussian Processes for Machine Learning2006